『2型糖尿病』は存在しない[5]データに語らせよ

コロンブスの卵

前回記事では，Ahlqvist博士が提唱した糖尿病の新分類は，HbA1cなどの指標を『数値に基づいて分類した』のではなく，先入観を排除して，ただ『似た者同士』のグループに分けただけなのに，それぞれのグループには，かなり特徴があることを紹介しました．

『2型糖尿病と一口に言っても，病態・症状は多種多様』とは昔から言われてきたことでした． しかし Ahlqvist博士の提案する新分類を見ると，『なぜ，これに気づかなかったのだろうか？』『どうして誰もこれをできなかったのだろうか？』と 不思議になります．

データに語らせた

人に語らせるのではなく『データに語らせよ』という言葉があります． 先入観で決めつけるのではなく，データ自身が表していることを客観的に解釈することこそが真実への近道という意味でしょう．

Ahlqvist博士の提案した新分類は斬新なものでしたが，それは正に『データに語らせた』からでしょう．

2型糖尿病をいくつかの類型に分類するという試みは，実際 過去から多数行われてきました．
2型糖尿病と呼ばれる患者の症状・病態を見ると，どうみても均質な集団ではなく多種多様だからです．

たとえば，糖尿病以前の段階ですら，空腹時血糖値障害(IFG= Impared Fasting Glucose)と耐糖能障害(IGT= Impaired Glucose Tolerence）とがあり，これらはまるで別物ではないかと考える人も多いです． IFGはたしかに空腹時血糖値は高いのですが，食後血糖値はむしろ健全であり，本格的に糖尿病を発症するリスクは，正常人とほとんど同じです． 一方空腹時血糖値は正常なのに食後血糖値が高い IGTは，ほぼ確実に糖尿病の前段階と見て間違いないでしょう．この段階ですでに2種類あるのです．

そこでこれまでの糖尿病を分類するアプローチでは，2型糖尿病の発症と進行に関連する，すべての確認済の(及び 考えられる) 生化学的変化から理論的に考えるものばかりでした．

一例をあげれば，下の図のように；

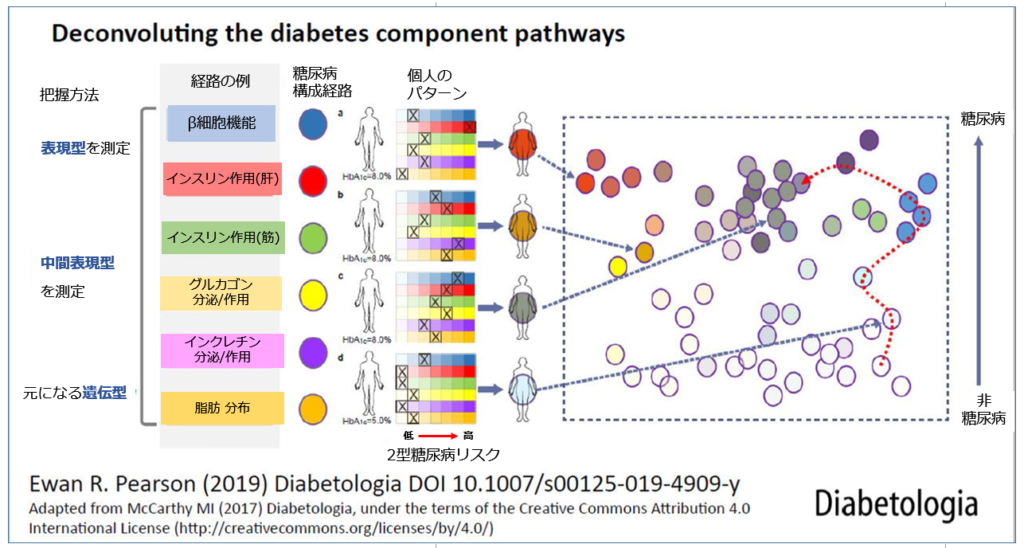
糖尿病の発症・進行について，ありとあらゆる 要因を生化学的に整理したうえで，糖尿病患者の症状が多種多彩なのは，それらの構成成分の割合が違うからだ，という考えです． ちょうど たかだか数種類のアルコール類から，その『配合割合』によって 無数のカクテルが作れるのと同じです．

ところが，このアプローチは糖尿病のメカニズムを研究するにはいいのですが，いざ目の前の個々の糖尿病患者を分類しようとすると，いちいちその人のDNA全解析から始まって，ありとあらゆる検査を行う必要があります． たとえそれをすべて行ったとしても，検査不能の項目(構成要素間の関連強度など）がありますから，推測に頼る部分もでてきます． つまり研究はできても，診断・治療には向いていません．

ところが Ahlqvist博士の行った方法は，まさにその正反対でした． 『データ同志が似た者同士を呼び集める』，ただこの単純な作業だけを行ってみたら，データが それぞれに特徴のある集団に 勝手に分かれていきました．まさにデータ自身が『語った』のです．

[6]に続く