『血糖値変動にかかわるすべての臓器の動作を数式で表して解析する』これが HOmeostasis Model Assessment(恒常性モデル評価)です.
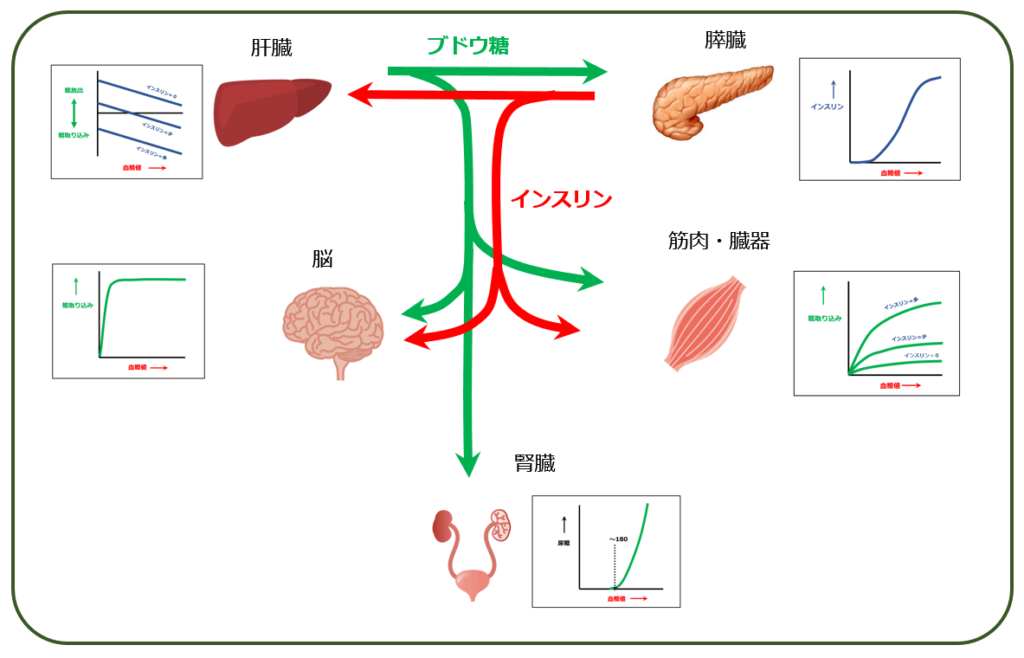
血糖値が高くなれば,インスリン分泌が多くなり,各組織での糖取り込みが増えます. その結果,多少血糖値が下がると,それに対応して多少インスリン分泌も減って・・・という複雑に絡み合った実際の変動も,すべてが数式で表されているのならば,どこで平衡に達するのかが計算できます.
これは 現在であればコンピュータで一瞬にして計算できますが, HOMAが考案された1970年代には,まだ大型電算機の時代でしたから,この計算は非常に困難でした.したがって最初に論文発表された時は,一部 計算式を簡略化しています.
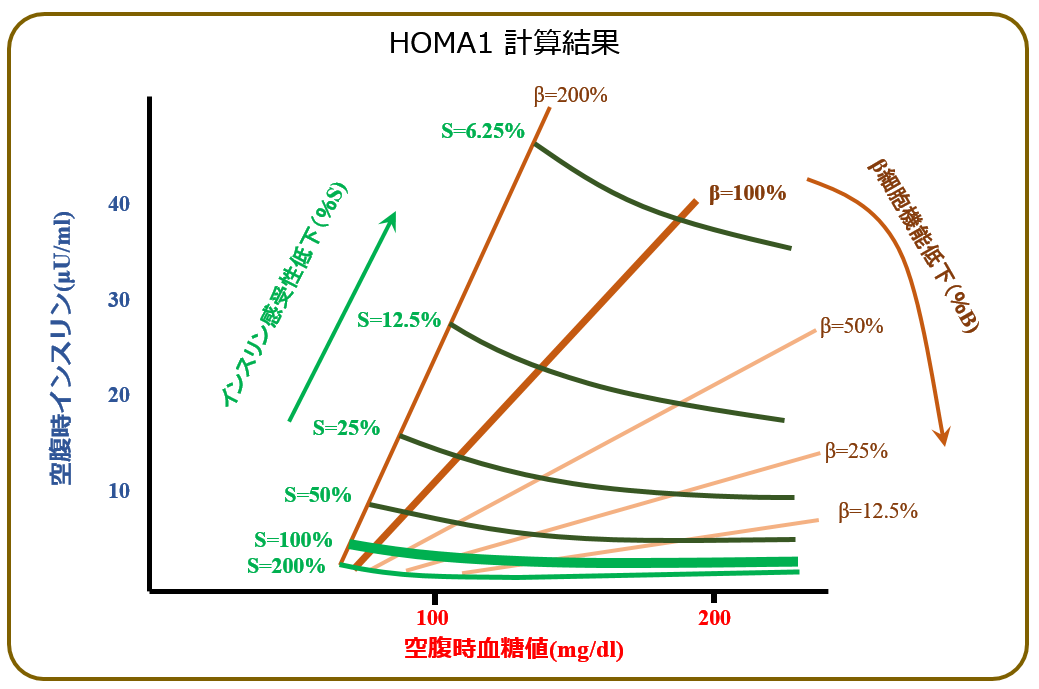
そして,それぞれの関係臓器が平衡状態に達した時(=典型的には空腹時)の血糖値とインスリン値が算出されました.これが恒常性モデルです.結果はこうなりました.
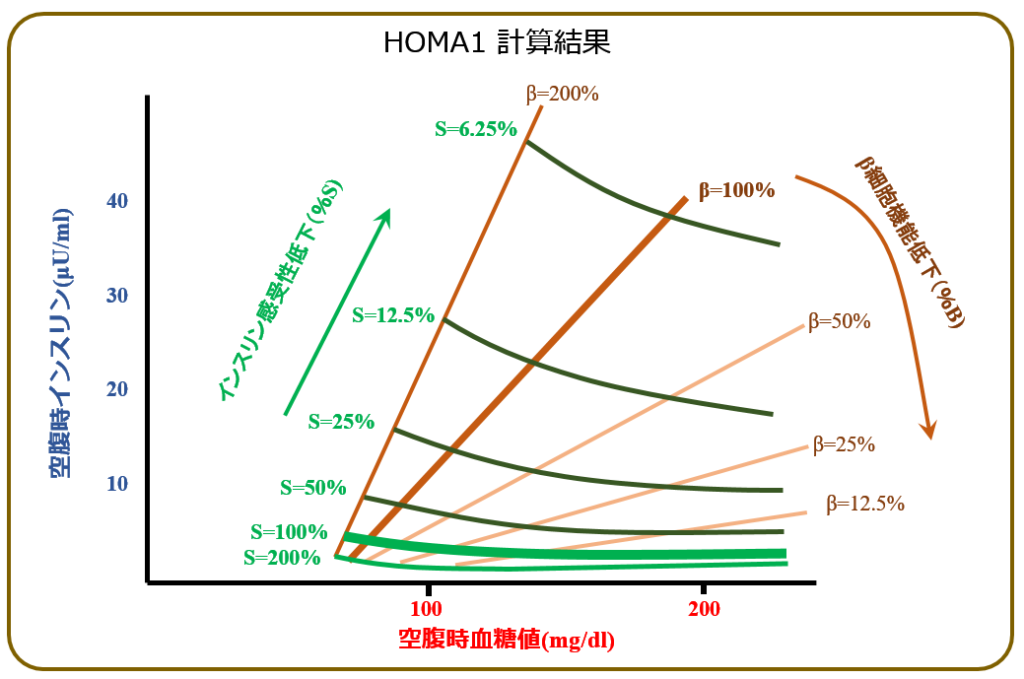
空腹時の血糖値(横軸)と,空腹時のインスリン値(縦軸)との 関係が表されています.
グラフは,インスリン感受性(=インスリン抵抗性の逆数)の大小,及び 膵臓β細胞機能の高低によって,複数の線が算出されています.
逆推定していく
この計算結果を用いて,空腹時の血糖値とインスリン値(IRI)から,逆に 膵臓β細胞のインスリン分泌能や,人体のインスリン感受性(インスリン抵抗性)を逆推定したものが,HOMA-βと HOMA-Rです.
グラフは こういう風に使います.
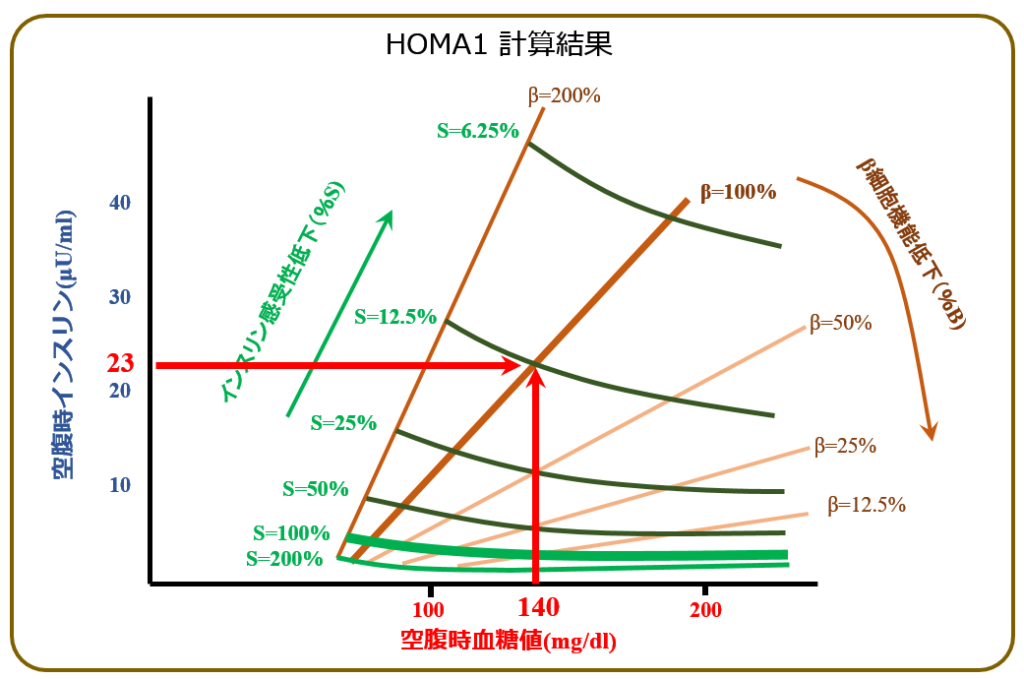
ある患者の空腹時の 血糖値[横軸]=140 で,インスリン値 [縦軸]=23であったとします.すると,これをグラフに当てはめると,この人のインスリン感受性(%S)は 平均健常者の12.5%,つまり1/8くらい(よってインスリン抵抗性は,その逆数の 8.0)で,膵臓機能(%B)は ほぼ平均健常者並の100%ほどと見積もれます.
もちろん,このグラフは,クランプ試験などの実データをベースにしているとはいえ,基本的には 数値モデルでシミュレーションした推算ですから,(実際には存在するであろう)個人差は一切無視したうえでの話です.
HOMA-Rで簡易化
ただ,これでも 結構煩雑なチャートです. したがって,実際には 上記のグラフの曲線をもっと簡単な式で近似したものが使われています.これが HOMA-R式です.

この式をグラフ化するとこうなります.
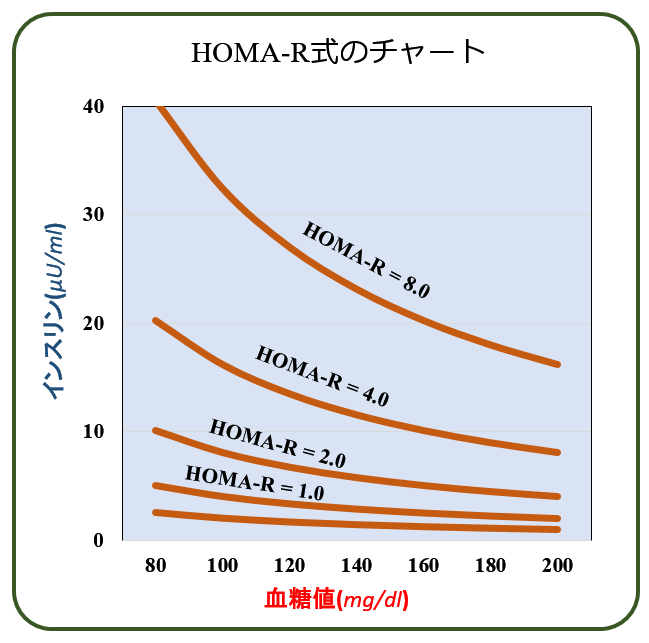
オリジナルのHOMAグラフとよく似ていますね. 本来のHOMAチャートと,この簡易化したHOMA-R式とを比較するとこうです.
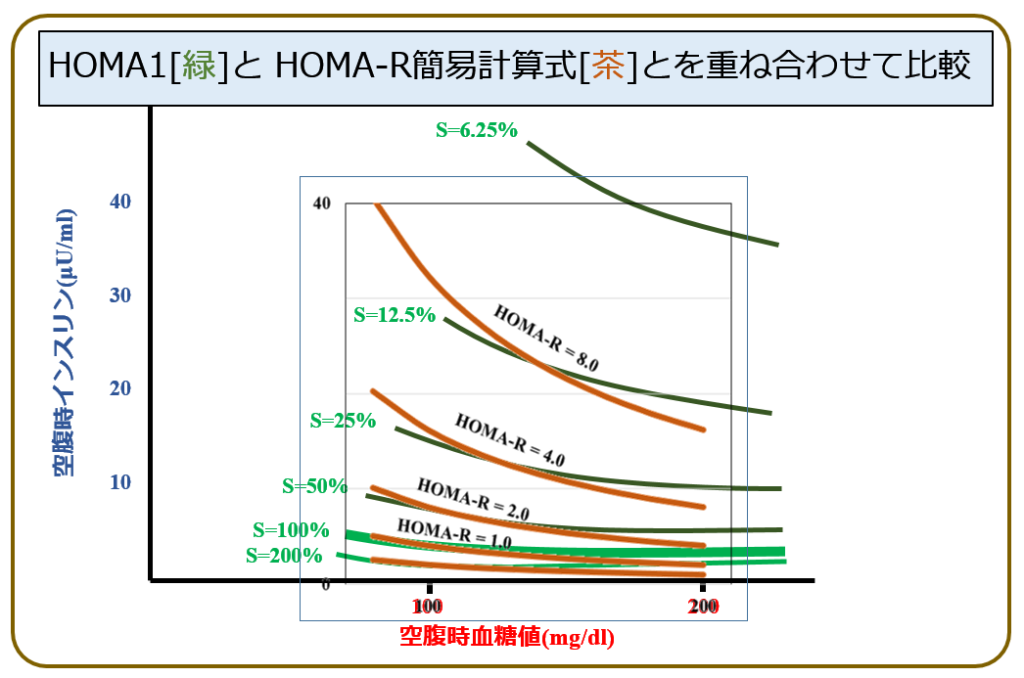
かなりよく近似できていることがわかります.これであれば,患者の空腹時の血糖値とインスリン値だけを知るだけで,その患者のおおよそのインスリン抵抗性を推測できます.しかし,これはあくまでも推定値です.
しかし,ここまでの話でおわかりのように,HOMA-Rの式は,あくまでもHOMAに近似した値を算出できる簡易推算式です. HOMAそのものではありません.
また 文献などで,『HOMA-R式は,血糖値が140以上の場合は適用できない』などと書かれていますが,それはこの比較を見ると理解できます. 元の HOMAとのズレが,血糖値140を越えると大きくなって不正確だからです.
クランプ試験に近づくように数値シミュレーションで計算した結果(HOMA)の,さらにそれを簡略化したものが HOMA-R式ですから,『クランプ試験』とピタリ一致することなど望めません.あくまでもHOMAやHOMA-Rは目安なのです.
[6]に続く


コメント